Overview
Finite Element Analysis (FEA) is a powerful tool for evaluating complex structural problems. Like all analytical software, bad results stem from bad input. We call it the “Garbage in, Garbage Out” principle of FEA.
Sometimes, with perfect inputs, you can still get the wrong answer using FEA. There are a lot of ways that your finite element analysis can take a wrong turn. Some of the most common issues include:
- Bad Mesh
- Poorly Applied Boundary Conditions
- Bad Contacts and Connection
So how do you know if your results are correct?
The answer is validation and verification (V&V). V&V is a process used to make sure that the FEA model behaves according to the laws of physics.
The Validation & Verification Process
First lets clarify these terms:
- Verification is the process of developing a computational model that accurately represents the underlying mathematical model and its solution.
- Validation is the process of of determining that a computational model accurately represents the underlying mathematical model and its solution.
The V&V process is incorporated into the analysis process. For this post let’s look at Verification Process as it relates to FEA. We’ll cover Validation in another post.
- Conceptual Model: A “napkin sketch” of the area of interest. The conceptual model consists of loads, boundary conditions and expected system response.
- Mathematical Model: The equations and initial conditions needed to describe the conceptual model. In a simple beam bending example this could be Euler beam theory.
- Computational Model: Correlates the mathematical solution into a discrete numerical solution software. The computational model is comprised of a software-specific the input file.
- Code Verification: Typically the domain of internal software developers. This verification process ensures that the software code algorithms are working correctly.
- Simulation Results: With the code verified; the computational model is solved. Simulation results are extracted from the computational model.
- Calculation Verification: Verification ensures that the simulation results match the solution of the mathematical model.
Verification Example
I find that principals are best applied through practice. Let’s consider verification of a model of a steel beam subject to uniform loading.
Conceptual Model
Our conceptual model is a steel beam with a rectangular cross section (2″x8″) that spans 10 feet. The beam carries a 30,000lb distributed load. It is simply-supported, with pin and pin-roller supports.
Mathematical Model (Hand Calculations)
We can predict the beam’s behavior using Euler–Bernoulli beam theory. Mathematical solutions predict that the beam will deflect 0.273 inches under load. The greatest stress in the beam is 21.1ksi. Download supporting hand calculations here.
Computational Model (Finite Element Model)
We develop a finite element model of the beam using over 30,000 eight-noded elements. Our model includes
- Distributed load on top surface
- Pin-end supports at the ends of the beam
- Lateral bracing to eliminate secondary buckling.
Code Verification
We developed our computational model using LS-DYNA a general-purpose finite element program. This software is developed by LSTC under a software quality assurance program. LSTC is responsible for verifying the code algorithms. In our example, code verification of commercial software is outside of our scope.
Simulation Results
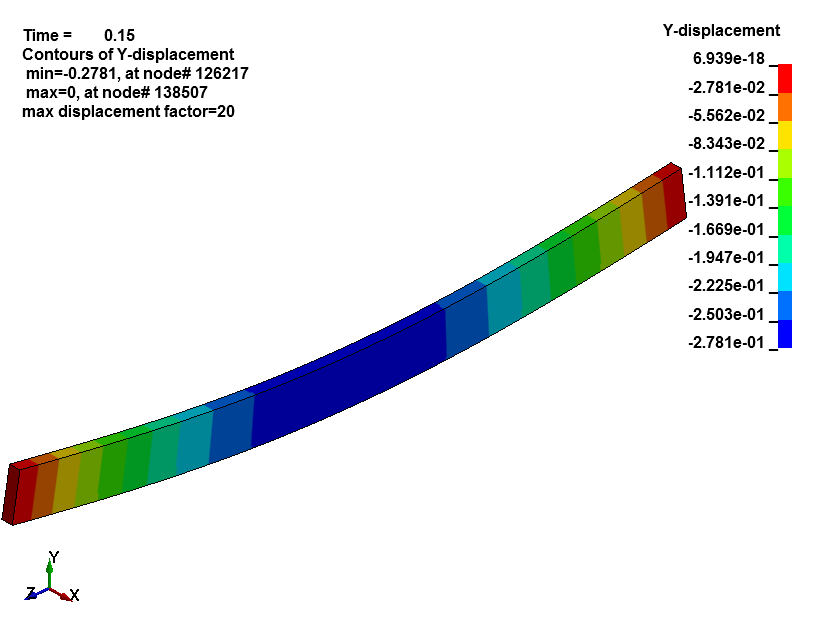
Our finite element model shows that the beam will deflect 0.277 inches at the center of the span.
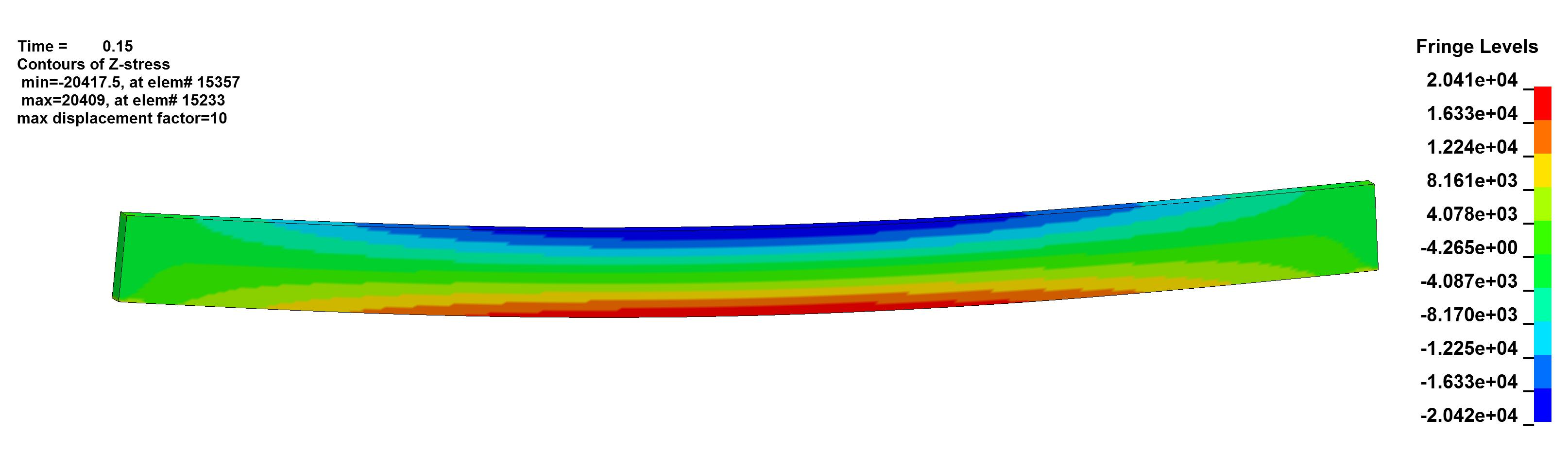
The greatest volumetric z-stress calculated in the beam is 20.4 ksi
Calculation Verification
We must verify our solution results. When validating I find it best to work from qualitative to quantitative assessments. This method minimizes hours expended on verification
Qualitative Assessment: First we ensure that the model behaves as expected. In our example, some qualitative parameters include:
- Peak vertical displacement located at the center of span
- No vertical displacement at ends of beam
- Peak stresses are in the center of span at the outer most fiber.
Notice we’re concerned with directions and trends, not magnitudes.
These observations agree with basic Euler–Bernoulli beam theory. We’re headed in the right direction. If they didn’t the computational model is most likely flawed. Additional troubleshooting may be required before progressing.
Quantitative Assessment: With the model behaving as expected, we can compare the magnitude of our results. In our example numerical solutions within 2% of theoretical will are acceptable.
- Deflection: The maximum deflections of the finite element model is 0.277″. The maximum deflection using Euler–Bernoulli beam theory is 0.273″. This corresponds to an error of 1.5% which is acceptable given our acceptance criteria. This error is far less when considering significant figures. The difference in predicted deflection is only 1/30,000 of the span.
- Stress: The maximum stress in the beam is 20,417 psi. The maximum bending stress using Euler–Bernoulli beam theory is 21,094 psi. This corresponds to an error of 3.2% which is unacceptable given our acceptance criteria.
How in a linear stress analysis could we predict the deflection, but be so off in the prediction of stress?
FEA reports the average stress in the element, which is 1/4″ thick. For a constant cross-section, stress is reported at a point 1/8″ from the edge. Recalculating resultant Euler–Bernoulli stress at a point 1/8″ from the edge, stress is 20,434 psi. This corresponds to an error of 0.08% which is acceptable given our acceptance criteria.
The computational model and simulation results agree the mathematical model. The FEA model can is verified with respect to theory.
Results Still Don’t Agree?
If the results didn’t agree, we would need to perform some troubleshooting. Some troubleshooting techniques we could utilize include:
- Mesh Fidelity: Re-mesh model to a finer mesh
- Inputs: Review key material parameters such as Modulus of Elasticity
- Supports: There should be no deflection at supports.
- Connections: A clear load path through members should be evident.
Conclusion
A FEA model and its results must be verified against theory and the mathematical model. In our example, hand calculations of beam using bending theory verify the results of our FEA.
At XCEED we know that FEA can become the analytical basis behind costly or high-risk decisions. Our FEA results need to be 100% accurate and verifiable by others. That’s why we verify using alternate calculations on all projects.
2 thoughts on “Finite Element Analysis Verification”
Doing mathematical solution manually , whatever it is, is good thing because the knowledge will be kept refreshing but sometimes when you are doubtful with your answer, it will be good if you can have some reference or guidance to make sure your solution is correct. So calculator would be handy in this case. Plus, if you are on doing it on a very short time, calculator would really help you save time.