Background
It’s a battle as old as Finite Element Analysis.
How do you achieve accurate results while balancing size and solve time of a FEA model?
Simple models may solve quickly, but are the results accurate? And, complex models may provide very accurate results, but solve time could be hours or even days.
Why?
Numerical software packages solve problems using a series of discrete points. Each point, or node, adds degrees of freedom (DOF) to the system. So the more DOFs in the model the better it will capture the structural behavior.
Each DOF adds complexity and increases solve time. The engineer needs to balance the complexity of the model with solve time:
-
Too few DOFs and the response could be incorrect
-
Too many DOFs and the model could take days to run
So how does an engineer develop an accurate but efficient FEA model?
By assessing convergence and demonstrating mesh independence.
Convergence and Mesh Independence Study
It doesn’t take much for a finite element analysis to produce results. But, for results to be accurate, we must demonstrate that results converge to a solution and are independent of mesh size. To begin, let’s define a few key terms:
-
Convergence: Mesh convergence determines how many elements are required in a model to ensure that the results of an analysis are not affected by changing the size of the mesh. System response (stress, deformation) will converge to a repeatable solution with decreasing element size.
-
Mesh Independence: Following convergence, additional mesh refinement does not affect results. At this point the model and its results are independent of the mesh.
A mesh convergence study verifies that the FEA model has converged to a solution. It also provides a justification for Mesh Independence and additional refinement is unnecessary.
Mesh Convergence Example
I find that principals are best applied through practice. Let’s consider convergence of a finite element model of a steel beam. We previously looked at finite element model verification within our blog, Finite Element Analysis Verification.
Analysis
Convergence studies varies the sizing and configuration of the FEA mesh. So before beginning, we disable the automatic meshing capability of our FEA solver.
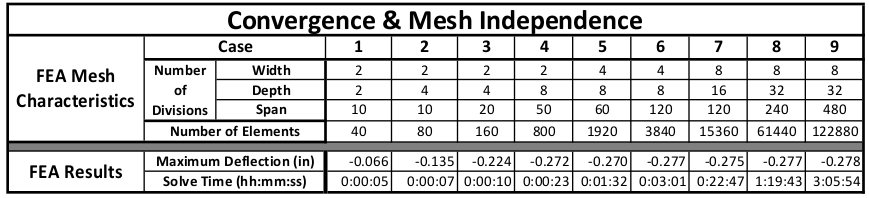
Our example is a rectangular beam so we can vary mesh parameters in three directions. We can vary by element size or number of divisions. For our example we will use “number of divisions” with equal spacing. Our mesh will vary the number of elements along:
-
Beam Width
-
Beam Depth
-
Beam Span
Process
Using an iterative method, we increase the number of elements along each side and solve. We record the complexity of the model vs. response. For us, complexity is the number of elements and subsequent degree of freedom. Our response of interest is the maximum vertical deflection. Varying the number of elements along each edge, we can develop a table of mesh size vs deflection and solve time:
Insight
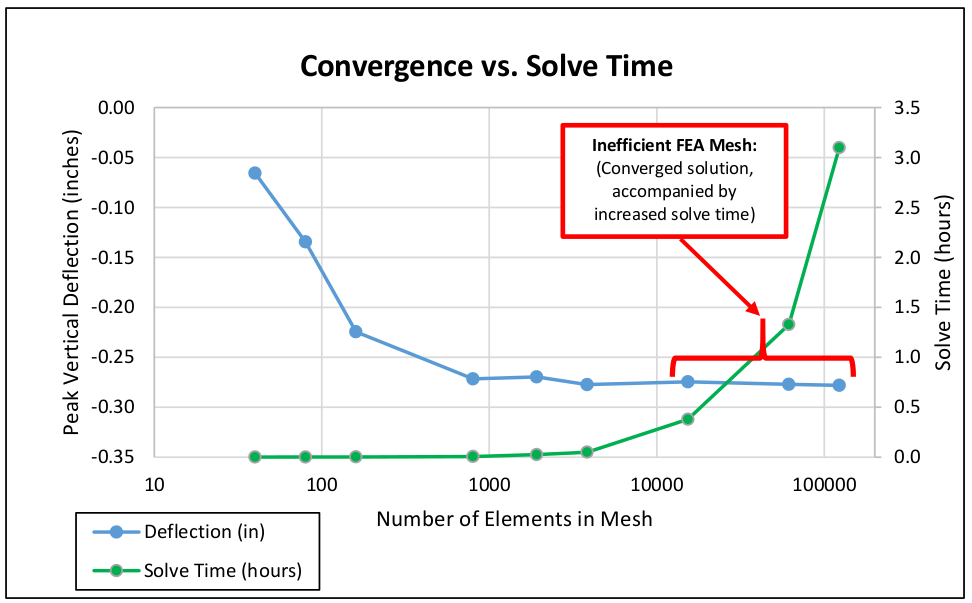
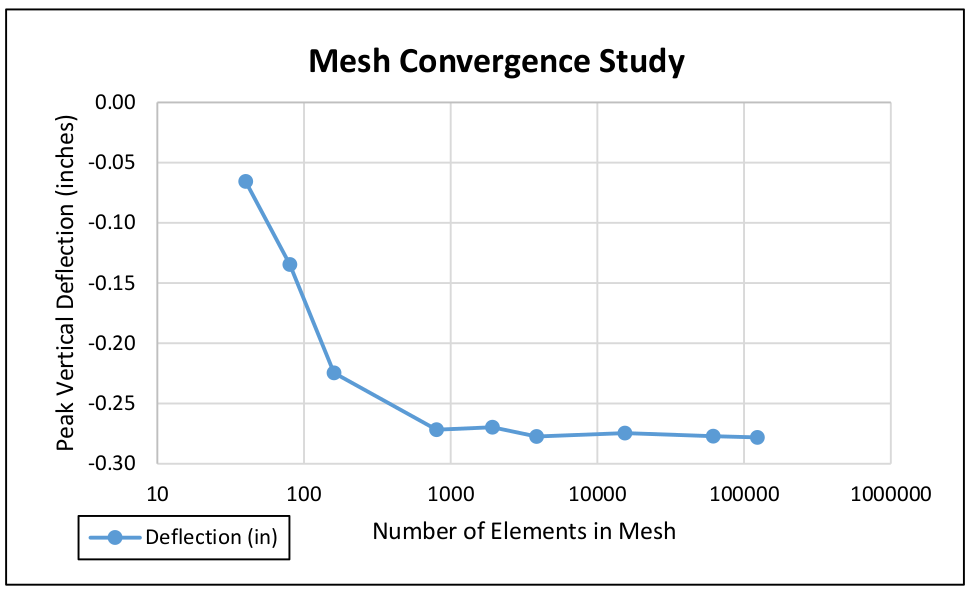
We can then plot maximum vertical deflection vs. the number of elements in the model. At a point, the response of the system converges to a solution. Refinement of the mesh (the addition of more elements) has little to no effect on the solution.
When this occurs we have a converged solution.
Solve Time
We also can plot solve time and vertical deflection vs. the number of elements. The addition of elements increases solve time. At a point, more elements increases solve time with no refinement in solution. Refinement past this point is an inefficient application of FEA.
Conclusion
The results of an FEA model must be independent of mesh size. A convergence study ensures the FEA model captures the systems behavior, while reducing solve time.
At XCEED we know that FEA can become the analytical basis behind costly or high-risk decisions. Our FEA results need to be 100% accurate and verifiable by others. That’s why we perform a mesh convergence on all projects to verify the accuracy of our results.